Friday´s Hill, Haslemere, 24 de junho de 1902
Prezado colega,
Agradeço-lhe pela sua carta e pelo envio de seus trabalhos. Enviei-lhe novamente as coisas que foram perdidas no correio. Eu já tinha corrigido o erro na página 7 do seu [livro] Begriffsschrift. Mas, como Senhor disse, ele não tem qualquer consequência nociva.
Eu sou da opinião que se pode variar, em geral, conceitos e que a contradição somente surge quando o próprio argumento é uma função da função, ou seja, quando a função e o argumento não podem variar independentemente. Na função ϕ{ε’ϕ(ε)}, ϕ é a única variável e o argumento ε’ϕ(ε) é ele próprio (segundo o modo usual de expressão) uma função de ϕ. Parece que funções da forma ϕ{F(ϕ)}, onde F é uma constante e ϕ, uma variável, são certamente permitidas para qualquer valor de ϕ, embora seja perigoso quando a extensão está em questão. Eu as chamei de formas quadráticas: poder-se-ia estar inclinado em introduzir um imaginário lógico ao imaginário algébrico. Imediatamente se obtém, em tais funções, uma função saturada quando se dá o valor de ϕ; todavia, elas não são funções de primeira ordem, nem têm argumentos constantes. A função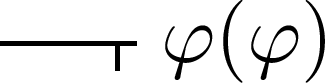 
leva a uma contradição semelhante a 
.
leva a uma contradição semelhante a .
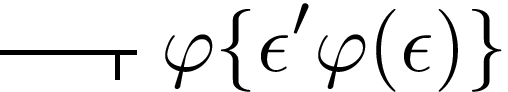Fui levado à contradição da seguinte maneira. Cantor, como o Senhor naturalmente sabe, provou que não existe o maior número cardinal [Anzahl]. Esta prova é como se segue: R∈1→1.∂´⊃Cls’∂.w = ∂ ∩ x э (x∼ ε ι∂´ x): ⊃R. w∼ε ∂ : ⊃. Nc’ Cls’ ∂ ≻ Nc’ ∂. (Esta é somente a parte mais essencial da prova). Mas há conceitos cuja extensão compreende tudo; portanto, tais conceitos deveriam ter o maior número cardinal. Eu tentei estabelecer uma relação biunívoca entre todos os objetos e todas as classes; quando empreguei a prova de Cant
or à minha relação especial, restou-me a classe Cls ∩ x э (x ∼ ε x), embora todas as classes já tivessem sido enumeradas. Durante um ano, eu refleti sobre esta contradição; Acredito que a única solução é variar, independentemente, função e argumento. A partir do que o Senhor disse na pág. 37, a saber, que um nome de função nunca pode ocorrer na posição de um nome próprio (eu estou falando do [livro] Grundgesetze), surge uma dificuldade filosófica. Eu sei muito bem que há boas razões para esta visão, mas ela se contradiz. Pois “ξ nunca pode ocorrer na posição de um nome próprio” é uma proposição falsa se ξ é um nome próprio, mas, caso contrário, ela não é, em geral, uma proposição. Se puder existir algo que não é objeto, então não podemos afirmar este fato sem contradição; pois, na afirmação, o algo em questão se torna um objeto. Portanto, parece-me duvidoso se podemos considerar ϕ em ϕx, em geral, como algo. Mas, neste ponto, mergulhamos na lógica filosófica.
or à minha relação especial, restou-me a classe Cls ∩ x э (x ∼ ε x), embora todas as classes já tivessem sido enumeradas. Durante um ano, eu refleti sobre esta contradição; Acredito que a única solução é variar, independentemente, função e argumento. A partir do que o Senhor disse na pág. 37, a saber, que um nome de função nunca pode ocorrer na posição de um nome próprio (eu estou falando do [livro] Grundgesetze), surge uma dificuldade filosófica. Eu sei muito bem que há boas razões para esta visão, mas ela se contradiz. Pois “ξ nunca pode ocorrer na posição de um nome próprio” é uma proposição falsa se ξ é um nome próprio, mas, caso contrário, ela não é, em geral, uma proposição. Se puder existir algo que não é objeto, então não podemos afirmar este fato sem contradição; pois, na afirmação, o algo em questão se torna um objeto. Portanto, parece-me duvidoso se podemos considerar ϕ em ϕx, em geral, como algo. Mas, neste ponto, mergulhamos na lógica filosófica.
O Senhor disse na pág. 49 que Γ=∆ tem uma referência quando Γ e ∆ são justamente ou nomes de percursos de valores ou nomes de valores de verdade.Contudo, não achei nas páginas precedentes nenhuma explicação de Γ=∆ para o caso em que um dos argumentos é um nome de percurso de valores e o outro é o nome de um valor de verdade, exceto para o caso em que o percurso de valores em questão compreende tudo ou nada. Mas acredito que não lhe entendi corretamente neste ponto.
Até agora eu li apenas seus [livros] Begriffsschrift e Grundgesetze: eu estudarei imediatamente os outros trabalhos.